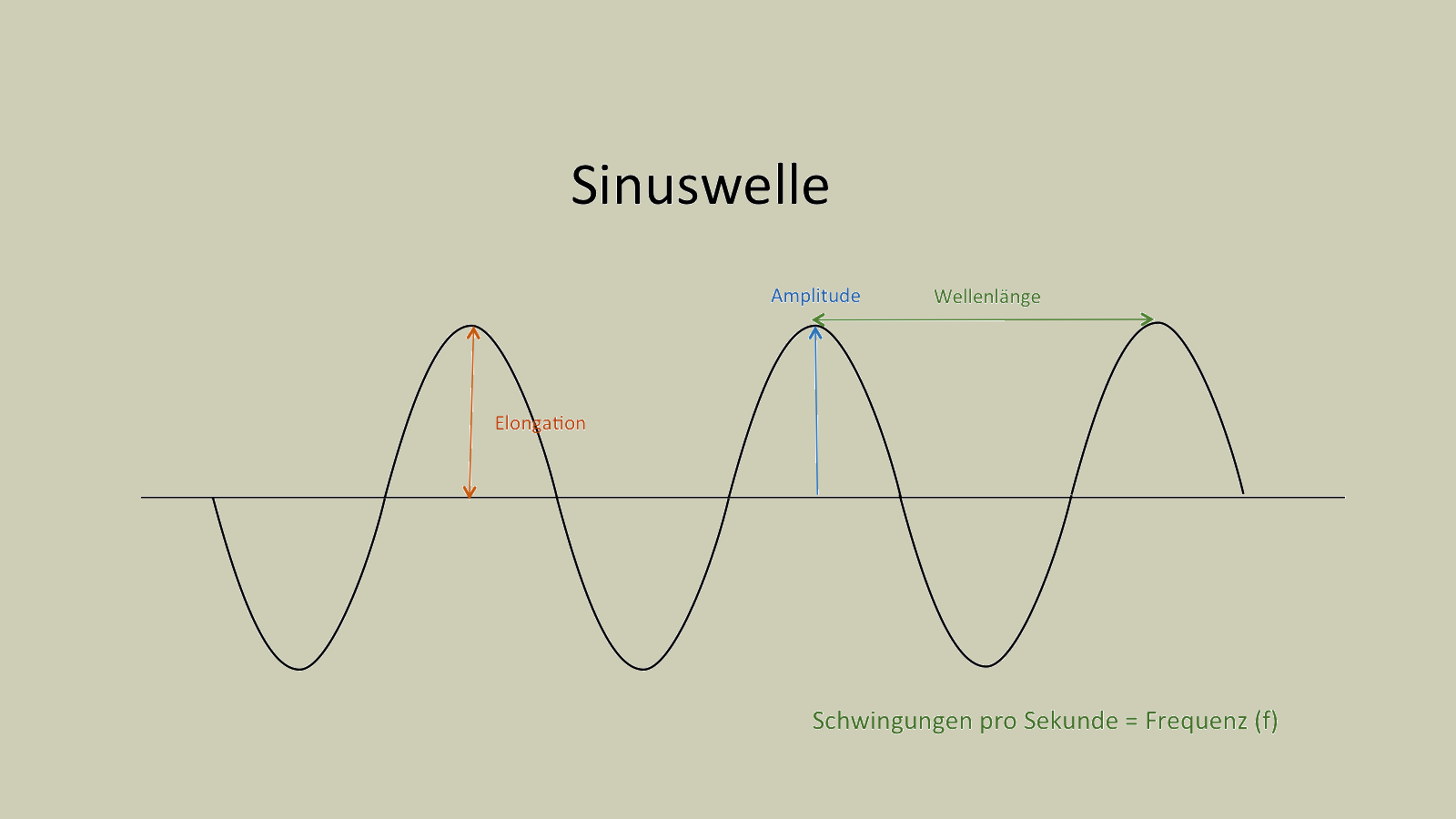
Was sind Phasenverschiebungen, was sind Interferenzen?
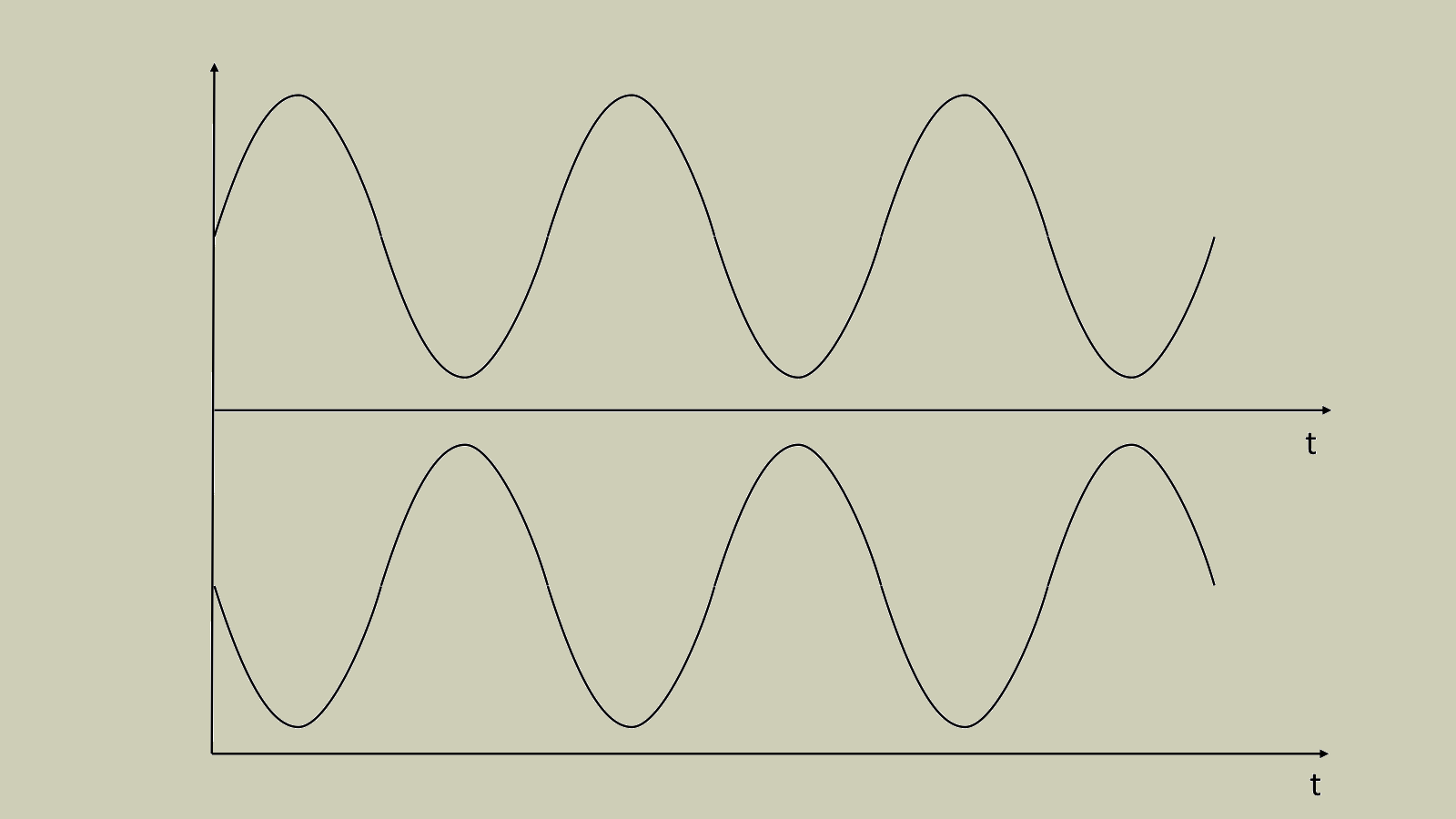
Wenn sich zwei Sinus-Schallwellen derselben Frequenz überlagern, kommt es abhängig von der Phasenlage der beiden Wellen zu einer Verstärkung oder Bedämpfung. Eine solche Überlagerung wird Interferenz („Überlagerung“) genannt. Haben beide Schallwellen dieselbe Phasenlage und dieselbe Amplitude, kommt es bei der resultierenden Welle zu einer Verdopplung der Amplitude. Ist die Phasenlage bei einer der beiden Wellen um genau 180° im Vergleich zur anderen bei gleicher Amplitude gedreht („invertiert“), kommt es zu einer kompletten Auslöschung der Amplitude. Der Ton ist nicht mehr zu hören. Werden zwei identische Signale mit einem komplexen Frequenzspektrum aus zahlreichen Sinusschwingungen, etwa von einem Instrument*, zeitverzögert zusammengemischt, kommt es aufgrund zahlreicher verschiedener Phasenlagen-Verhältnisse bei einigen Frequenzen zu Bedämpfungen und Auslöschungen, während andere verstärkt werden. Das Signal wird also verzerrt. Die dabei entstehenden tiefen Kerben im Frequenzgang sehen auf einem typischen Analysegerät wie die Zinken eines Kamms aus. Daher heißt diese Art der Verzerrung auch Kammfilter-Effekt, den wir gleich näher erläutern werden. Vorher aber wird die Stehende Welle unser Thema sein, die ebenfalls zur Kategorie der Interferenzen gehört. Stehende Wellen wirken sich auf den Bassbereich aus. Sie sind in Ton-Regien besonders problematisch und daher außerordentlich unbeliebt.
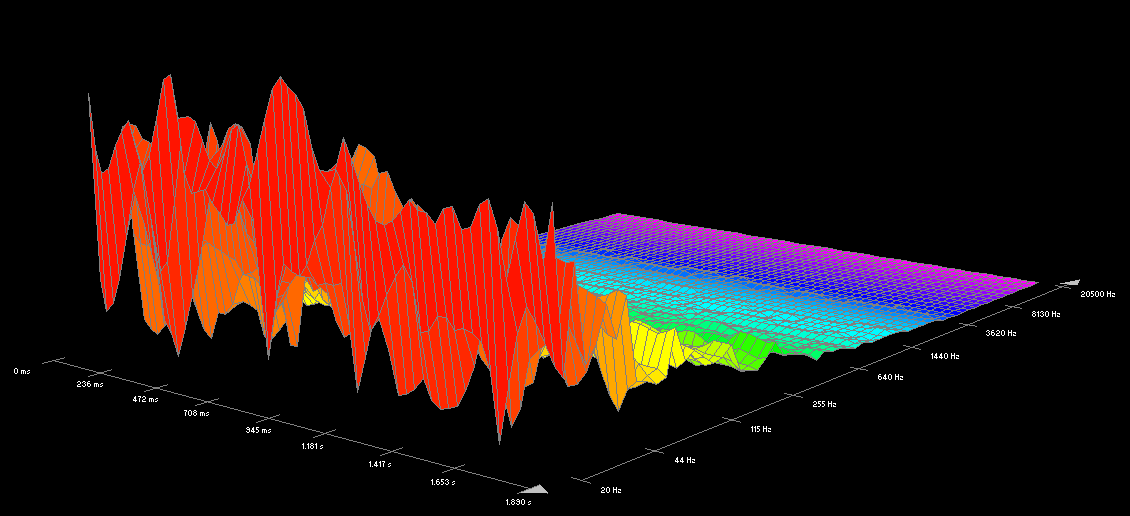
Was ist der Frequenzgang?
Mit dem Frequenzgang ist die spektrale Zusammensetzung eines Klanges oder Geräusches gemeint. Jede einzelne Frequenz kann als ein Sinuston angesehen werden. Jeder Instrumententon besteht also aus zahlreichen verschiedenen, unterschiedlich lauten Sinustönen. Welche Frequenzen, also welche Sinustöne, das Signal mit welcher Lautstärke enthält, kann mit einem speziellen Frequenz-Analysegerät visualisiert werden. Dies ist vielleicht am ehesten mit einem Prisma vergleichbar, das die einzelnen Frequenzen weißen Sonnenlichts sichtbar machen kann. Frequenzanalysegeräte gehören zu den wichtigsten Werkzeugen beim Mischen. Allerdings wird mit zunehmender Übung auch Ihr Gehör bald in der Lage sein, spektrale Zusammensetzungen zumindest annährend zu identifizieren.
Was ist ein Pegel?
In der Audiotechnik wird häufig von Pegeln gesprochen. Wenn jemand etwas mehr Pegel geben soll, heißt das meistens, er soll einen Mischpultkanal etwas lauter machen. Tatsächlich steht beispielsweise an Mischpultkanälen, Lautstärkereglern oder Equalizerbändern die Maßeinheit dB für Dezibel. Dezi- ist hierbei ein Präfix wie bei Dezimeter. Die eigentliche Maßeinheit heißt also Bel. Verwendet wird allerdings fast ausschließlich das Dezibel.
Das Dezibel wird in der Audiotechnik zwar oft synonym als Einheit für Lautstärke verwendet, ist aber eigentlich etwas ganz anderes. Im Grunde handelt es sich nicht einmal um eine richtige Maßeinheit, sondern ein dimensionsloses Vergleichsmaß ähnlich dem Prozent. Man sagt auch Hilfsmaßeinheit dazu. Der entscheidende Unterschied ist, dass Prozent ein lineares Vergleichmaß ist, Dezibel ein logarithmisches. Logarithmische Vergleichsmaße machen dann Sinn, wenn ein mit dem Vergleichsmaß zu erfassender Wertebereich besonders groß ist und die Verwendung üblicher linearer Maßeinheiten daher sehr unhandlich wäre.
In anderen Worten: Man hat also mit sehr kleinen und gleichzeitig sehr großen Zahlen zu tun, mit denen sich schwer arbeiten lässt, weil sich diese beispielsweise nicht vernünftig in einem Koordinatensystem (oder eben an einem Mischpultfader) darstellen lassen. Bei der Bildung eines Pegels wird der große Wertebereich mithilfe einer logarithmischen Rechenvorschrift stark komprimiert. Beim Pegel werden per Definition die Werte immer in das Verhältnis zu einem vordefinierten Bezugswert gesetzt, der oftmals mit einer prägnanten physikalischen Eigenschaft verbunden wurde, und durchlaufen die logarithmische Vorschrift. Die Werteintervalle stehen danach nicht mehr in einem linearen, sondern in einem logarithmischen Bezug zueinander. Werden zwei Werte ohne fixen Bezugspunkt in ein logarithmisches Verhältnis gesetzt, spricht man nicht mehr von Pegel, sondern von Maß.
In der Audiotechnik haben wir mit allen möglichen Pegeln zu tun. Es gibt zum Beispiel Spannungspegel (dBv oder dBu) zur Vereinfachung von Volt-Wertebereichen oder etwa den Schalldruckpegel (DBSPL) zur Vereinfachung von Pascal-Wertebereichen. Ein besonderer Pegel ist der Digitale Aussteuerungspegel. Er kann per Definition nicht positiv sein.

Hierzu ein Beispiel: Der Schalldruck, auch „Schallwechseldruck“* (*Wir erinnern uns – die Luftdruckunterschiede am Trommelfell), der für die Hör-Empfindung verantwortlich ist, wird für gewöhnlich nicht in der für Druck üblichen Maßeinheit Pascal, sondern als Schalldruckpegel angegeben (dBSPL). Das hat folgenden Grund: Das Ohr kann schon sehr geringe Schalldrücke wahrnehmen, aber auch sehr hohe (bevor es Schmerzsignale sendet). Mit steigender Lautstärke nimmt also die Empfindlichkeit sehr stark ab. Würde man den Wertebereich in der herkömmlichen linearen Maßeinheit Pascal angeben, wäre er sehr groß. Die Hörschwelle liegt bei nur 20 Mikropascal, also 20 Millionstel Pascal (bei 2 kHz). Die Obergrenze des Ertragbaren, die sogenannte Schmerzschwelle, liegt aber bei 100 Pascal. Dieser Druckwert entspricht dem sage und schreibe Zweimilliardenfachen des Drucks, der nötig ist, um vom Gehör als Geräusch identifiziert zu werden. Man hat also allen Grund, die Schalldruck-Empfindung des Gehörs über eine logarithmische Rechenvorschrift zu komprimieren und so handlich zu machen.
Also hat man einen Bezugswert definiert und festgelegt, dass die Hörschwelle bei 20 Mikropascal den Beginn einer logarithmischen Hilfsskala bilden soll. Sie entspricht also 0 dBSPL. Die anderen Werte werden nun in das Verhältnis zum Bezugswert gesetzt und anschließend logarithmiert. 1 Pascal, ein bereits ordentlicher Schalldruck und das Zwanzigmillionenfache der Hörschwelle, entspricht nun 94 dBSPL. Für die Schmerzschwelle von 100 Pascal können synonym in der Pegelskala 134 dBSPL angegeben werden.
Typische Schalldruckpegel ausgewählter Schallquellen
| Schallquelle | Entfernung zur Schallquelle | Schalldruck in Pascal |
Schalldruckpegel dBspl |
| – | |||
| Düsenjet | 30 m | 630 Pa | 150 dB |
| Schuss | 1 m | 200 Pa | 140 dB |
| Schmerzschwelle | am Ohr | 100 Pa | 134 dB |
| Düsenflugzeug | 100 m | 6,3 – 200 Pa | 110 – 140 dB |
| Presslufthammer | 1 m | 2 Pa | 100 dB |
| Gehörschäden bei längerer und wiederholter Beschallung | am Ohr | ab 0,36 Pa | 85 dB |
| Hauptverkehrsstraße | 10 m | 0,2 – 0,63 Pa | 80 – 90 dB |
| Auto | 10 m | 0,02 – 0,2 Pa | 60 – 80 dB |
| Sprache | 1 m | 2 · 10−3 – 2 · 10−2 Pa | 40 – 60 dB |
| Ruhiger Raum | am Ohr | 2 · 10−4 – 6,3 · 10−4 Pa | 20 – 30 dB |
| Leises Atmen | am Ohr | 6,32 · 10−5 Pa | 10 dB |
| Hörschwelle (2000 Hz) | am Ohr | 2 · 10−5 Pa (20 µPa) | 0 dB |
Quelle: Wikipedia
Lassen Sie sich hier vom Begriff „Logarithmus“ nicht verunsichern. Wirklich mit Pegeln rechnen müssen Sie bei der Mischung nicht. Es schadet allerdings nichts, wenn Sie wissen, dass Mischpultregler aus oben genannten Gründen über logarithmische dB-Skalen verfügen (meist dBu). 0 dB entsprechen per Definition der Neutral-Einstellung (Unity Gain), was bedeutet: Das Signal wird weder bedämpft noch verstärkt. Negative dB-Werte entsprechen einer Bedämpfung und positive einer Verstärkung. Die dabei entstehenden empfundenen Lautstärke-Unterschiede lassen sich prima über den Daumen peilen. Eine Erhöhung des Pegels an einem Mischpult um 6 dBu entspricht ungefähr einer Verdopplung der empfundenen Lautstärke, eine Absenkung des Pegels um 6 dBu einer Halbierung der empfundenen Lautstärke. Merken sollten Sie sich vor allem den letzten Satz.